机器一直想知道的关于金属氧化物半导体电容器的一切

机器学习(ML)通常被定义为模仿人类智能能力的数据驱动技术，它通过经验一点一点地提升其准确性。它从收集大量的数据开始，比如数字、文本、图像等等。在使用数据进行训练后，机器学习算法建立一个逻辑模型，通过尽可能少的人为干预来识别模式。在样本训练数据的帮助下，程序员在引入新数据集之前测试模型的有效性。训练数据越多，预测越好。

然而，如果训练数据集有偏差、不一致甚至是错误的，我们就不能期望对新数据的可靠模式或预测。但随着这一领域的迅速扩张，我们可以通过强制执行始终遵循自然规律的物理框架来约束ML模型。

在我们最近在《应用物理杂志》上的工作中，我们开发了一个这样的物理约束ML模型，以深入了解金属氧化物半导体(MOS)电容器的静电，这是当前CMOS(互补金属氧化物半导体)技术的基本构建块。

MOS电容器由掺杂的半导体体、薄绝缘体(即氧化物)和称为栅极的金属电极组成。根据所施加的栅极电压的值，它以三种模式工作:积累，耗尽和反转。在积累模式下，类似掺杂型的移动电荷载流子在氧化物-半导体界面处积累形成薄层。

随着栅极电压的增加，界面的移动电荷逐渐耗尽，留下极性相反的固定离子。它在半导体表面引起一个扩大的电位下降。随着栅极电压的进一步升高，在氧化物-半导体界面下形成一层浓度相近的倒掺杂型移动电荷载流子。因此，我们说MOS电容已经进入反转模式。

MOS电容器的静电是由泊松-玻尔兹曼方程(PBE)控制的，这是一个高度非线性的微分方程(DE)。DE表示一个或多个自变量的函数及其导数之间的相互关系。函数表示一个物理量，导数表示相对于自变量的变化率。

在计算机上求解非线性微分方程更可取，因为解析解通常比较棘手。标准技术(如有限差分法、有限元法、射击法、样条法)和基于这些技术的用户友好软件包可用于求解各种de。

神经网络(NNs)是ML的一个子集，最近在几个科学和工程学科中产生了重大影响，可以毫不费力地解决非线性DEs。他们在类似人类大脑的分层结构中使用相互连接的节点，使生物神经元相互传递信号。

神经网络可以准确地逼近复杂的多元函数，并能很好地解决多变量问题传统的技术，例如，依赖于有限元方法和样条的离散化。神经网络的主要缺点是训练速度慢，计算量大基因表达让人筋疲力尽。然而，随着计算和优化技术的改进，我们已经战胜了这一挑战。在这里，我们研究机器是否可以通过使用ML求解PBE来学习MOS电容器的物理原理。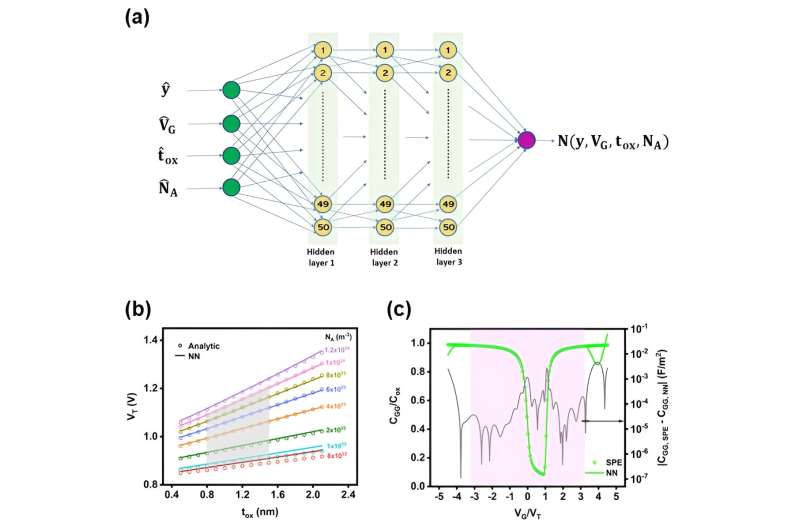

一种名为PINN(物理信息神经网络)的方法已经成为解决物理科学(汉堡方程，薛定谔方程等)引起的DEs的非常流行的方法。尽管它非常通用，可以用于处理任何DE，但在PINN中边界条件(bc)并不是硬约束的。

相反，它们与DE一起作为惩罚组合到损失函数中，损失函数计算ML模型中预测值和实际值之间的差异。因此，不能保证完全满足bc。另一方面，Lagaris等人提出了另一种技术来规避这个问题。

它使用控制方程来找到一个适合DE的试解，这种方法完全满足bc。然而，没有一个通用的程序来构建这样的试解，特别是对于我们所面临的复杂的边界条件，在一个MOS电容器的情况下。

我们解决MOS电容器PBE的方法是由PINN和Lagaris等人的方法驱动的。到目前为止，后一种方法被用来生成诺伊曼和狄利克雷bc的试验，这相对简单。相比之下，我们的PBE既需要简单的Dirichlet BC，也需要涉及函数及其衍生物的复数Robin BC。

尽管其具有高度非线性的性质，但我们表明，使用Lagaris等人的方法以满足PBE的两个bc的函数形式(即以一个或多个函数作为参数的函数)构建试验解是具有挑战性的，但也是可能的。在我们的模型中，我们对设备的物理域进行了精确采样，以从试验解中构造损失函数。

样品的数量决定了损失函数计算的复杂性和优化试验。因此，我们设想了一种基于物理的采样方案，并将器件参数随机引入模型。这种方法帮助模型获得了极高的准确性。

我们用Python中可用的传统数值方法以及行业标准的表面电位方程(SPE)验证了我们的模型。

通过这项研究，我们发现我们的NN模型可以学习输入变量(即半导体的厚度、栅极电压、氧化物厚度和掺杂浓度)与半导体电势之间的关系。

此外，除了解释积累、耗尽和反转机制外，它还能够捕获MOS器件物理的几个相关方面，如掺杂依赖的耗尽宽度、阈值电压随氧化物厚度和掺杂的变化以及低频电容电压特性。该模型即使在采样域之外也继续服从器件物理。

总之，我们首次报道了机器学习模型在不使用任何标记数据的情况下复制MOS电容器基本物理特性的可能性(与典型的监督机器学习相反)。我们发现，由于泊松-玻尔兹曼方程的唯一边界条件所构成的动态性，常用的PINN方法无法学习泊松-玻尔兹曼方程。

我们制定了一个自然满足边界条件的参数模型，以便利用神经网络的表达能力来获得具有特殊精度的解决方案。此外，我们表明，所提出的模型可以准确地捕获关键的见解，如耗尽宽度，阈值电压，反转电荷等。

这个故事是科学X对话的一部分，研究人员可以在这里报告他们发表的研究文章的发现。请访问此页面了解有关ScienceX对话框的信息以及如何参与。

更多信息:Tejas Govind Indani等人，MOS电容器静电的物理约束学习，应用物理杂志(2023)。DOI: 10.1063/5.0168104期刊信息:Journal of Applied Physics

Tejas Indani曾是一名理科硕士。班加罗尔印度科学学院(IISc)学生。Kunal Narayan Chaudhury是班加罗尔印度科学研究所的副教授。Sirsha Guha是班加罗尔印度科学研究所(IISc)的博士生。Santanu Mahapatra是班加罗尔印度科学研究所的教授。主页:sites.google.com/site/kunalnchaudhury/home faculty.dese.iisc.ac.in/santanu/